0
  1. شما اینجا هستید:  
  2. صفحه اصلی
  3. تارنگار
  4. معرفی ماژول AC/DC در کامسول

معرفی ماژول AC/DC در کامسول

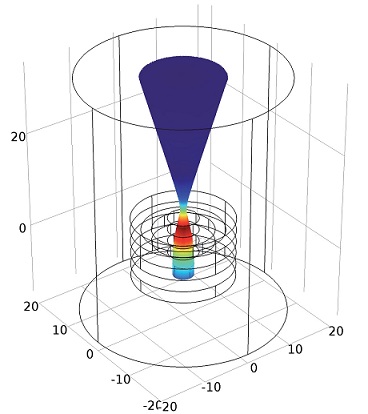
 ماژول AC/DC برای شبیه سازی میدان های الکتریکی، مغناطیسی و الکترومغناطیسی در حالت ایستا یا کند تغییر (ادواتی با ابعاد در حدود بیشتر از یک دهم طول موج امواج الکترومغناطیسی) جهت طراحی و بهینه سازی انواع ادوات الکترومغناطیسی از قبیل خازن، القاگر، سیم پیچ، موتور الکتریکی، محرک و سنسور‌ استفاده می‌شود.

 

 

 

با استفاده از این ماژول می‌توان پارامترهایی مانند میدان‌ها، گشتاورها و نیروهای الکترومغناطیسی، مقاومت، ظرفیت، القاییدگی، امپدانس، توان اتلافی و ... را در سیستم‌های الکتریکی و مغناطیسی خطی و غیر خطی، همسانگرد و ناهمسانگرد، برای حالت‌های پایا، وابسته به زمان و حوزه فرکانسی محاسبه نمود. بعلاوه به کمک این ماژول می‌توان نتایج شبیه‌سازی‌های ۲ و ۳ بعدی را به عنوان قطعه‌ای از یک مدار الکترونیکی استفاده نمود و قطعه شبیه‌سازی شده را در یک مدار قرار داد و رفتار مدار الکتریکی را بررسی نمود.

شبیه‌سازی در این ماژول بر پایه حل معادلات ماکسول انجام می‌شود و بسته به نوع فیزیک انتخابی کامسول تغییراتی در آن ایجاد می کند.

\[ \mathbf {\nabla} \cdot \mathbf{D} = \rho\]

\[\mathbf{\nabla} \cdot \mathbf{B} = 0\]

\[\mathbf{\nabla} \times  \mathbf{E} = - \frac{\partial \mathbf{B}}{\partial t}\]

\[\mathbf{\nabla} \times  \mathbf{H} = \mathbf{J} +\frac{\partial \mathbf{D}}{\partial t}\]

در روابط بالا E بردار شدت میدان الکتریکی، D بردار جابجایی الکتریکی (چگالی شار الکتریکی)، H بردار شدت میدان مغناطیسی، B بردار چگالی شار مغناطیسی، J بردار چگالی جریان الکتریکی و ρ چگالی بار الکتریکی است.

بعلاوه کامسول بسته به فیزیک انتخاب شده، از روابط ساختاری زیر استفاده می‌کند:

\[ \mathbf {D} = \epsilon \mathbf{E}\]

\[ \mathbf {B} = \mu \mathbf{H}\]

\[ \mathbf {J} = \sigma \mathbf{E} + \mathbf{J_0}\]

در روابط فوق J0 بردار چگالی جریان خارجی، σ چگالی بار سطحی، ϵ گذردهی الکتریکی مورد و μ تراوایی مغناطیسی محیط مورد بررسی می‌باشد.

با توجه به نوع فیزیک، کامسول از اشکالی از معادلاتی مانند پایستگی بار الکتریکی و روابط بین پتانسیل‌ها و میدان‌های الکتریکی و مغناطیسی استفاده می‌کند.

\[ \mathbf {\nabla} \cdot \mathbf{J} = - \frac{\partial \rho}{\partial t}\]

\[ \mathbf{B} = \mathbf{\nabla} \times \mathbf{A} - \nabla V_m\]

\[ \mathbf{E} = - \nabla V - \frac{\partial \mathbf{A}}{\partial t}\]

در معادلات بالا V پتانسیل الکتریکی، Vm پتانسیل اسکالر و A پتانسیل برداری میدان مغناطیسی است.

در ماژول AC/DC بسته به نوع مسئله، شرایط مرزی مختلفی از جمله پتانسیل الکتریکی یا مغناطیسی، عایق الکتریکی و مغناطیسی، مقدار بار، جریان و میدان صفر، ترمینال (جهت اتصال مرزها به مدار)، شرط مرزی دوره‌ای (برای سامانه‌های متناوب)، جریان سطحی و ... را می‌توان بر فضای شبیه‌سازی اعمال نمود. علاوه بر شرایط مرزی ذکر شده، این ماژول قابلیت شبیه‌سازی سامانه‌هایی با ابعاد نامتناهی را نیز دارد.

حوزه کاربردهای این ماژول در طراحی، شبیه‌سازی و بهینه‌سازی انواع سیم پیچ‌ها، سیم لوله‌ها، جوشکاری الکتریکی، عایق‌های الکتریکی، سازگاری الکترومغناطیسی (EMC)، تداخل الکترومغناطیسی (EMI)، حفاظ‌های الکترومغناطیسی، ماشین‌های الکترومکانیکی، مدارهای الکترونیکی، کوره‌های القایی، خازن‌ها، دی‌الکتریک‌ها، موتور‌ها، ژنراتور‌ها، آهنرباهای دائمی، پیستون‌های مغناطیسی، سنسور‌ها، ترانسفوماتور‌ها و القاگرها است.

 

 

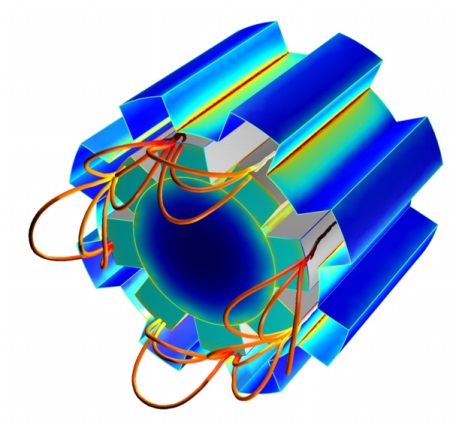
از فیزیک‌های موجود در این ماژول می‌توان به موارد زیر اشاره نمود:

 

جریان‌های الکتریکی (Electric Currents)

این فیزیک به محاسبه میدان الکتریکی و توزیع جریان و پتانسیل الکتریکی در محیط‌های رسانا در شرایطی که اثرات القایی قابل صرف نظر کردن باشد، می‌پردازد. این مسئله به شکل‌های حوزه فرکانسی، پایا و وابسته به زمان قابل حل است. معادلات دیفرانسیل حاکم بر فیزیک جریان‌های الکتریکی معادله پایستگی بار بر اساس قانون اهم است که با حل آن پتانسیل الکتریکی (V) بدست می‌آید.

 

\[ \nabla .{\mathbf J}=Q_j \]

\[ {\mathbf J}=\sigma {\mathbf E}+\frac{\partial {\mathbf D}}{\partial t}+{{\mathbf J}}_e \]

\[ {\mathbf E}=-\nabla V \]

در معادلات بالا Qj منبع جریان و Je چگالی جریان خارجی است.

 

جریان‌های الکتریکی پوسته‌ای (Electric Currents, shell)

در این فیزیک، میدان الکتریکی و توزیع جریان و پتانسیل الکتریکی در پوسته‌های رسانای نازک در شرایطی که اثرات القایی قابل صرف نظر کردن باشد، محاسبه می‌شود. بدین منظور در فیزیک جریان‌های الکتریکی پوسته‌ای برای پوسته‌های دو و سه بعدی مسئله به شکل‌های حوزه فرکانسی، پایا و وابسته به زمان قابل حل است. مانند فیزیک جریان‌های الکتریکی، معادلات دیفرانسیل حاکم بر این فیزیک، معادله پایستگی بار بر اساس قانون اهم است که با حل آن پتانسیل الکتریکی (V) بدست می‌آید.

\[{\nabla }_T.\left(d_s{\mathbf \ }{\mathbf J}\right)=d_s\ Q_j\]

\[{\mathbf J}=\sigma {\mathbf E}+\frac{\partial {\mathbf D}}{\partial t}+{{\mathbf J}}_e\]

\[{\mathbf E}=-{\nabla }_{{\rm T}}V\]

 

مدار‌های الکتریکی (Electrical Circuit)

این فیزیک برای مدل‌سازی جریان‌ها و ولتاژهای مدارات الکترونیکی بکار می‌رود و شامل ادواتی مانند منابع جریان و ولتاژ، مقاومت، خازن، القاگر و ادوات نیمه رسانا است. فیزیک مدارات الکتریکی قوانین پایستگی کیرشف را برای حالت‌های دامنه فرکانسی، وابسته به زمان و پایا حل می‌نماید.

 

الکترواستاتیک (Electrostatics)

این فیزیک برای محاسبه میدان الکتریکی، جابجایی الکتریکی و توزیع پتانسیل الکتریکی در مواد دی‌الکتریک در شرایطی که توزیع بارهای الکتریکی مشخص باشد می‌باشد. از آنجایی که مسائل مورد بررسی در این فیزیک استاتیک است، حل مسئله به روش پایا صورت می‌گیرد. با اینحال امکان استفاده از این ماژول برای حالت‌های حوزه فرکانسی، زمانی و ویژه فرکانس نیز وجود دارد که در کوپل شدن با دیگر فیزیک‌ها قابل استفاده است. معادله‌ای که در این فیزیک حل می‌گردد، قانون گاوس است که با حل آن پتانسیل الکتریکی به صورت میدان اسکالر بوجود می‌آیند.

 

\[\nabla .{\mathbf D}={\rho }_v\]

\[{\mathbf E}=\ -\nabla V\]

 

شبیه‌سازی میدان مغناطیسی اطراف یک آهنربا با کامسول

 

میدان‌های مغناطیسی (Magnetic Fields)

فیزیک میدان‌های مغناطیسی برای محاسبه میدان‌های مغناطیسی و توزیع جریان القایی در انواع سیم‌پیچ، سیم‌لوله، رسانا و آهنربا‌ها بکار می‌رود. این فیزیک برای حالت‌های پایا، حوزه فرکانسی و وابسته به زمان قابل حل است. معادلات دیفرانسیل مورد بررسی در فیزیک میدان‌های مغناطیسی معادلات ماکسول است که برای پتانسیل برداری مغناطیسی فرمول‌بندی شده است.

\[\sigma \frac{\partial {\mathbf A}}{\partial t}+\nabla \times {\mathbf H}={{\mathbf J}}_e\]

\[{\mathbf B}=\nabla \times {\mathbf A}\]

 

فرمولبندی میدان مغناطیسی (Magnetic Field Formulation)

فیزیک میدان‌های مغناطیسی برای محاسبه میدان‌های مغناطیسی و توزیع جریان القایی در انواع مواد مغناطیسی است. این فیزیک برای شبیه‌سازی زمانی ادوات غیر خطی (E-J) مانند ابررساناها مناسب می‌باشد بنابراین رسانندگی در تمامی نقاط مورد شبیه‌سازی در این فیزیک باید غیر صفر باشد. این فیزیک برای حالت‌های پایا، حوزه فرکانسی و وابسته به زمان قابل حل است. معادلات دیفرانسیلی که در فیزیک میدان‌های مغناطیسی حل می‌شوند، معادلات ماکسول است که برای میدان مغناطیسی فرمول‌بندی شده است.

\[\nabla .{\mathbf B}=0\]

\[{\mathbf J}=\nabla \times {\mathbf H}\]

\[\nabla \times {\mathbf E}=\ -\frac{\partial {\mathbf B}}{\partial t}\]

 

میدان‌های مغناطیسی بدون جریان (Magnetic Fields, No Currents)

این فیزیک برای شبیه‌سازی مسائل مغناطواستاتیک است و به کمک آن می‌توان میدان‌های مغناطیسی ناشی آهنرباهای دائمی و دیگر منابع میدان مغناطیسی را بررسی نمود. مسائل مورد بررسی به شکل پایا قابل حل‌اند. با اینحال برای کوپل شدن با دیگر فیزیک‌های کامسول حل وابسته به زمان نیز برای این فیزیک قابل افزوده شدن است. در این فیزیک قانون گاوس برای پتانسیل مغناطیسی حل می‌گردد.

 

\[{\mathbf H}=\ -\nabla V_m+{{\mathbf H}}_b \]

\[\nabla .{\mathbf B}=0\]

در معادله فوق Hb میدان مغناطیسی زمینه (background) است.

 

میدان‌های مغناطیسی و الکتریکی (Magnetic and Electric Fields)

این فیزیک برای محاسبه میدان مغناطیسی و توزیع جریان‌های الکتریکی است. در این فیزیک معادلات ماکسول بر حسب پتانسیل مغناطیسی برداری و پتانسیل الکتریکی حل می‌گردد. حل این معادلات به شکل حوزه فرکانسی و پایا امکانپذیر است.

 

ماشین‌های چرخان مغناطیسی (Rotating Machinery, Magnetic)

این فیزیک برای طراحی و بررسی موتور‌های الکتریکی و ژنراتورها کاربرد دارد. در این فیزیک معادلات ماکسول برای بدست آوردن پتانسیل برداری و اسکالر مغناطیسی حل می‌گردند.

 

رد‌یابی ذرات باردار (Charged Particle Tracing)

این فیزیک برای مدلسازی مسیر حرکت ذرات باردار تحت نیروهای الکترومغناطیسی است. از مزیت‌های این فیزیک شبیه‌سازی دوطرفه ذرات و میدان‌های الکترومغناطیسی است به این معنی که ذرات باردار برمیدان الکترومغناطیسی و میدان الکترومغناطیسی بر ذرات اثر می‌کند. از کاربردهای این فیزیک می‌توان به طراحی شتابدهنده‌ها، لنزهای الکترومغناطیسی، لوله‌های خلا و تجهیزات کاشت یون اشاره نمود. معادلاتی که در این فیزیک حل می‌گردند، معادلات حرکت مکانیکی ذره تحت نیروی الکترومغناطیسی است.

\[\frac{d\left(m_p{\mathbf v}\right)}{dt}={{\mathbf F}}_t\]

در این معادله mp جرم ذره، v سرعت آن و Ft نیروی خالص وارد بر آن است.

 

شبیه‌سازی لنز الکترومغناطیسی با کامسول